Why the Grand Relativity Theory? (Part III)

One of the significant physicists' misconceptions about nature is the uniqueness of time. When physicists encounter higher-multidimensional surroundings in their theory, they instinctively assign the extra-dimensions (beyond the ordinary four) as spatial. This premise, regarding the inequality of space and time footing, is evidence against the relativity principle.

The string theory, which had its origins in experimentally observed features of the strong force, requires the existence of six compactified extra spatial dimensions (a) and the four known spacetime dimensions. This presumption leads the theory to grave difficulties as it should deal with myriad different kinds of Callabi-Yau tiny manifolds or other similar bizarre things.

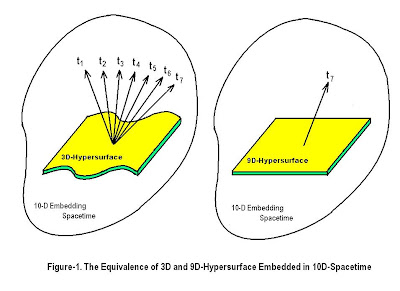
On the other hand, the grand relativity theory holds that the extra dimensions are temporal; thus, circumventing such complexities. Therefore, we may regard a system such as our world consisting of a 3D-space (hypersurface) embedded in 10D-manifold in which all extra dimensions are temporal ^b). Under the grand relativity theory, we have every right to transform it into, for instance, 9D-hypersurface embedding in the same 10D-manifold, by turning some of the temporal dimensions into spatial (Figure-1). The latter is exceedingly simpler than the former in terms of mathematical formulations, and yet it gives us the same solutions.

Physicists are used to oversimplifying their physical model using geometrical objects, such as 0D-point, 1D-line, and 2D-plane. However, one should be extremely cautious of using such objects, having no thickness at all as he or she probes more in-depth into the quantum realm.  At the quantum level, the range of actions could be concise, which might be approaching the object [quantum] thickness (at the range of 10^-33 to 10^-17 cm) ^c) that one deliberately ignores. It is no wonder that with such zero depth for their physical objects or models, physicists are confronting many irritating infinity problems.

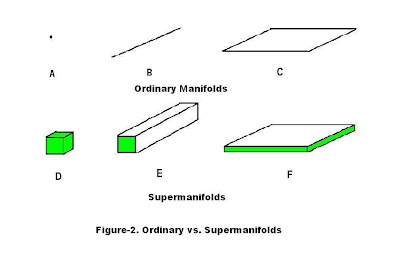
The grand relativity theory requires any physical objects or hypersurfaces having thicknesses, the number of which depends on the number of dimensions of the embedding manifold ^d) (Figure-2). However, physicists obliged to do a similar way by incorporating such forgotten thickness into their model called supersymmetry generators e).

In Brane theory, physicists assign some space and time's dimensions on and along its surface while off of it spatial. They certainly make a significant confusion as to the brane, like hypersurface embedding in a higher dimensional spacetime, should have solely spatial dimensions on and along its surface and temporal dimension[s] off of it.

The hypersurface or brane is the loci of things that co-occur if not at lower temporal dimensions it would certainly so at higher temporal dimension (Figure-3). 

The hypersurface tends to flatten out as it has higher dimensions. But how high should they be? Mathematically, a spacetime may embed an n-dimensional hypersurface properly only if the former has at least ½ n(n+1) dimensions. Our 4D-world, for example, requires a sufficient ample ambient space i.e., 10D-manifold, for having a complete degree of freedoms without being constrained at whatever directions.

It turns out that some theories, such as Supergravity, require an embedding spacetime of even higher dimensions. The Supergravity demands an eleven-dimensional ^f) embedding spacetime, but still, nobody can fully renormalize the Supergravity.

Notes:

a.  Physicists are assumed to be curled up into tiny loops as nobody ever directly experiences them.

b.   It can be expressed mathematically as Octonion, a Hypercomplex consisting of one real and seven imaginary variables. The real part is the spatial variables' function, while the seven imaginary parts represent seven different temporal dimensions.

c.  No real particle smaller than the hypersurface's thickness, except virtual particles perpetually emerge and submerge across the depth. This thickness size, which becomes the minimum size of the real particle is what physicists call hierarchy problem.

d.  Analogically under 3D-ambient space, a point has three thicknesses, string two thicknesses (cross-section), and plane one thickness. Otherwise, they would be evaporating into thin air.

e.  Mathematically physicists may express such a framework in terms of Superalgebra equation whose ordinary and super parts are sometimes called body and soul, respectively ¹. It is equivalent to Octonion Hypercomplex with its real and imaginary parts. Amazingly, this is a proper way to describe a subtle structure such as [higher dimensional] soul embedding a body, contrary to what most people think the soul is inside the body.

f.  It is a sort of pseudo dimension representing the tip of the 11+ "iceberg" dimensions. The ancients (among other Empedocles: 490-430 BC) described the realms consisting of earth, water, air, and fire analogous to a changing phase from ice, water, vapor, and steam.  We may interpret that earth representing energy/material stable things in 3D-space, water representing energy in 4D - 10D-spacetimes, the air in 11D - 55D-spacetimes and fire in 56D - 1540D-spacetimes, the dimension ranges of which are speculated under the ½ n(n+1) rule, if we may do so. This metaphor shows us that the energy associated with particular spacetime is hotter as the spacetime dimensions become higher. The reality beyond those dimensions is far from our wildest imagination and concern.

Why the Grand Relativity Theory? (Part II)

As the dimensions of a drop of water to its water substance, the dimensions of spacetime are the geometrical manifestation of a particular cosmic energy.  Our world, together with its multidimensional surroundings (grand cosmos), comes into existence as the natural manifestation of a broad spectrum of different cosmic energies ^a). 

How these multidimensional worlds come into being? It begins with the separation of positive and negative energy in the highest-dimensional world. This separation creates a hypersurface (space) of one lower dimension between the two opposite energies. The newly created hypersurface, in turn, splits in two, and so forth. Thus, the separation happens successively, creating many hypersurfaces (spaces) embedding one after another in descending order of their dimensions. 

The energy segregation in each world, however, doesn't happen instantaneously. The area of the hypersurface formed in between the two opposite energies broadens up gradually from a specific minimum size to what the current magnitude is (Figure-1). It is the underlying reality that makes our universe expanding ^b). 

This kind of phenomenon also explains why our world is flat ^c).  As such, we don’t require buying the concept of inflationary phase happened in the early life of the universe (at around 10^-35 to 10^-30 second after Big Bang) whose inflation rate is far exceeding the speed of light. Besides, the existence of energies at the surroundings of our universe (hypersurface) may explain the possible source of dark energy we miss so dearly.

The advantage of using hypersurface over the hyperspace is clear. With the former, we can easily describe objects such as fields propagating on its surface (classical fields) as well as those off its surface traversing through its thickness ^d) (quantum fields)^, as depicted in Figure-2. 

The interaction of the opposite energies generates those quantum fields which propagate across through the hypersurface. As the quantum fields hit the hypersurface's surface, they ignite quantum sparks ("quarks"), which we recognize as fundamental particles. These sparks (particles) together with the hypersurface (space) which they abode ^e) perpetually appear and disappear at the rate equal to the speed of light ^f). 

The two interacting opposite energies move at the different directions forcing the normal axis of the hypersurface to rotate around the grand perimeter of the spacetime at the speed of light ^g). This dynamic grand rotation creates what we perceive as time (Figure-3). 

The combination of these two phenomena makes our physical space, together with all matters it contains, disappears completely as one moment passes, and reappear as a completely different space as the next moment arrives ^h). Most physicists overlook this underlying reality, which reflects both the relativity and quantum realms.

The interactions of the opposite energies also make the hypersurface rotate around its normal axis. It rotates, in turn, all objects it contains from super-galaxies, galaxies, solar systems, planets down to atomic and subatomic realms.

Notes:

a. The ensemble of such grand cosmos can be mathematically expressed in the form of the Laurent series or depicted as the Riemann sphere.

b.   As shown by Riemann's annulus of convergence, the world can evolve only from a specific minimum size. It starts to get its stable form and expands to its maximum magnitude, beyond which it becomes precarious and tears apart into pieces doomsday. As nature abhors the singularity, do we need the Big Bang cosmology and black hole postulate?

c.   It is flat but locally curved and undulates due to the gravitation effect exerted by local concentrations of energy and mass.

d.   In the order of Planck distance i.e., 10^-33 cm or equivalent 10^-44 second, below which the hypersurface would disappear into thin air. Assuming a zero thickness of such hypersurface would lead us to many annoyance problems of infinity.

e. The separation of energy never creates a stable hypersurface between the two halves. Mathematically, in quantum mechanics, the square roots of the relativistic energy formula, E² = m²c⁴ + p²c², do not give a neat separation of its positive and negative roots. It means that physically, the split of the positive and negative energy never creates a stable interface (hypersurface) between them. It is ephemeral in the sense that it appears and disappears perpetually.

f.   It is just like sparks appear and disappear on the surface of large TV or computer screen. Amazingly, the display also appears and goes together with the flashes.

g. The energies’ movement as the result of their mutual interaction also makes the hypersurface rotate around its lateral axis resulting in a hyper-helical type of rotation. In a higher-dimensional ambient space, we can depict this hypersurface movement as a 3D-front wave propagating across the 4D-surface of a grand 5D-ocean.

h.    Heraclitus (500 BC) said that the world is in flux. We can never step into the same river twice. He also stated that the world was like a gigantic flame. At any instant, the fire we see is entirely different from the flame we saw just a moment ago. Everything in the world is always changing and yet is still exclusively itself.